Tri Khaerudin: Teori

Tampilkan postingan dengan label Teori. Tampilkan semua postingan

Jumat, 29 Mei 2020

Wireless Gigabit and Small Cell

A. Wireless Gigabit and Small Cell

Gigabit Wireless adalah nama yang diberikan untuk sistem komunikasi nirkabel yang kecepatan transfer datanya melebihi jangkauan atau melebihi satu gigabit (satu miliar bit) per detik. Kecepatan tersebut dicapai dengan modulasi sinyal yang kompleks, seperti modulasi amplitudo quadrature (QAM) atau sinyal yang menjangkau banyak frekuensi. Ketika sebuah sinyal merentang banyak frekuensi, fisikawan menyebut itu sinyal lebar pita lebar. Dalam industri komunikasi, banyak penyedia layanan Internet Nirkabel dan perusahaan telepon seluler menggunakan antena frekuensi radio nirkabel untuk memperbaiki jaringan inti, menghubungkan bisnis, dan bahkan rumah tempat tinggal individu.

Frekuensi dan band umum untuk Gigabit Wireless

Untuk detail lebih lanjut tentang protokol dan informasi dalam ruangan, lihat halaman IEEE 802.11ac dan WiGig . Secara umum, protokol dalam ruangan mengikuti standar lintas-vendor dan berkomunikasi dalam pita 2,4 GHz, 5 GHz, dan (segera) yang tidak berlisensi 60 GHz.

Protokol tautan pembawa luar ruang sangat bervariasi dan tidak kompatibel antar vendor (dan seringkali model dari vendor yang sama).

Catatan: perangkat bandwidth yang lebih tinggi membutuhkan modulasi yang tidak terlalu rumit untuk mencapai kecepatan tinggi.

Broadband Nirkabel

Penyedia layanan Internet (ISP) sedang mencari cara untuk memperluas layanan kecepatan tinggi gigabit per detik (Gbit / s) kepada pelanggan mereka. Ini dapat dicapai melalui serat ke arsitektur jaringan broadband tempat , atau alternatif yang lebih terjangkau menggunakan nirkabel tetap di mil terakhir dalam kombinasi dengan jaringan serat di mil tengah untuk mengurangi biaya penggalian kabel serat optik kepada pengguna. Di Amerika Serikat, pita 60 GHz V tidak berlisensi. Ini menjadikan V band pilihan yang menarik untuk digunakan sebagai akses nirkabel tetap untuk layanan Gbit / s untuk terhubung ke rumah dan bisnis. Demikian pula, 70/80 GHz E band dilisensikan ringan yang dapat lebih mudah diakses oleh lebih banyak penyedia untuk menyediakan layanan tersebut.

Ada beberapa pengadopsi awal dari pendekatan fiber-wireless hybrid untuk menyediakan layanan Gbit kepada pelanggan. Salah satu ISP itu adalah Webpass, sebuah perusahaan yang didirikan pada 2003 di San Francisco sebagai ISP nirkabel yang berfokus pada bangunan di kota-kota besar. Sejak itu, Webpass telah meningkatkan kecepatan seiring dengan peningkatan teknologi nirkabel. Pada 2015, Webpass menawarkan koneksi 1 Gbit / s ke pelanggan komersial, namun, pelanggan residensial terbatas pada kecepatan hingga 500 Mbit / s untuk berbagi tautan nirkabel 1 Gbit / s di antara banyak penghuni di gedung yang sama. Perusahaan menggunakan kombinasi berbagai band berlisensi dan tidak berlisensi.

Pada Januari 2016, sebuah perusahaan startup Starry dari Boston memperkenalkan Starry Point dengan tujuan untuk menyediakan kecepatan internet Gbit / s secara nirkabel ke rumah-rumah. Perangkat ini adalah unit nirkabel tidak bergerak yang terpasang pada jendela sebagai titik akses untuk terhubung ke jaringan inti Starry menggunakan komunikasi gelombang milimeter . Perusahaan itu tidak mengungkapkan rincian band tersebut, tetapi mengklaim sebagai “teknologi gelombang bertahap milimeter gelombang aktif pertama di dunia untuk komunikasi internet konsumen”. [15] Namun, pada Januari 2018, pada saat perusahaan mengumumkan perluasan layanan beta untuk mencakup 3 kota: Boston, Los Angeles , dan Washington, DC , kecepatannya masih terbatas hingga 200 Mbit / dtk. [16]

Pada Juni 2016, Google Fiber mengakuisisi Webpass untuk meningkatkan upayanya dalam eksperimennya dengan teknologi nirkabel. Alhasil, Google Fiber berupaya keras untuk tetap menggunakan fiber untuk mengeksplorasi lebih lanjut tentang alternatif nirkabel yang lebih murah. Pada awal 2017, divisi Webpass dari Google Fiber memperluas layanan nirkabel 1 Gbit / s kepada pelanggan di banyak kota di Amerika Serikat.

Pada November 2016, Atlas Networks, ISP yang melayani Seattle , menyebarkan layanan V-band Gbit / s kepada pelanggan dalam jarak 750 meter (0,47 mil) ke jaringan seratnya. Throughput maksimum untuk setiap koneksi adalah 1 gigabit per detik.

Pada bulan Oktober 2017, Cloudwifi, ISP pemula yang berbasis di Kitchener, Ontario mulai menggunakan pita tetap nirkabel 60 GHz untuk menyediakan konektivitas Gbit / s kepada pelanggan dalam jarak 2 kilometer (1,2 mil) dari titik koneksi seratnya.

Pada bulan Oktober 2017, Newark Fiber memungkinkan pelanggan pertamanya di Newark, New Jersey dengan layanan nirkabel tetap 10 Gbit / s. Newark Fiber menggunakan pemancar V-band 10 Gbit / s dengan jarak hingga 1,8 kilometer (1,1 mi).

Small Cell

Sel kecil adalah node akses radio seluler berdaya rendah yang beroperasi dalam spektrum berlisensi dan tidak berlisensi yang memiliki jangkauan 10 meter hingga beberapa kilometer. Mereka “kecil” dibandingkan dengan macrocell seluler, sebagian karena mereka memiliki jangkauan yang lebih pendek dan sebagian karena mereka biasanya menangani lebih sedikit panggilan atau sesi bersamaan. Mereka memanfaatkan spektrum yang tersedia dengan menggunakan kembali frekuensi yang sama berkali-kali dalam wilayah geografis. Lebih sedikit situs makrosel baru sedang dibangun, dengan jumlah yang lebih besar dari sel-sel kecil yang diakui sebagai metode penting untuk meningkatkan kapasitas jaringan seluler, kualitas dan ketahanan dengan fokus yang berkembang menggunakan LTE Advanced.

Jenis Sel Kecil

Sel-sel kecil dapat mencakup femtocell , picocell , dan sel mikro . Jaringan sel kecil juga dapat diwujudkan dengan menggunakan teknologi radio terdistribusi menggunakan unit baseband terpusat dan kepala radio jarak jauh . Teknologi Beamforming (memfokuskan sinyal radio pada area yang sangat spesifik) dapat lebih meningkatkan atau memfokuskan cakupan sel kecil. Semua pendekatan terhadap sel-sel kecil ini menampilkan manajemen pusat oleh operator jaringan seluler .

Sel-sel kecil menyediakan jejak radio kecil, yang dapat berkisar dari 10 meter di dalam lokasi perkotaan dan dalam bangunan hingga 2 km untuk lokasi pedesaan. Picocells dan microcell juga dapat memiliki jangkauan beberapa ratus meter hingga beberapa kilometer, tetapi mereka berbeda dari femtocell karena mereka tidak selalu memiliki kemampuan mengatur diri dan mengatur diri sendiri.

Sel-sel kecil tersedia untuk berbagai antarmuka udara termasuk GSM , CDMA2000 , TD-SCDMA , W-CDMA , LTE dan WiMax . Dalam terminologi 3GPP , Home Node B (HNB) adalah femtocell 3G. Home eNode B (HeNB) adalah femtocell LTE. Wi-Fi adalah sel kecil tetapi tidak beroperasi dalam spektrum berlisensi dan karenanya tidak dapat dikelola seefektif sel kecil yang menggunakan spektrum berlisensi. Penempatan sel kecil bervariasi sesuai dengan kasus penggunaan dan teknologi radio yang digunakan.

Istilah Payung

Bentuk sel kecil yang paling umum adalah femtocell. Mereka awalnya dirancang untuk penggunaan bisnis perumahan dan kecil, dengan jangkauan pendek dan sejumlah saluran. Femtocell dengan jangkauan dan kapasitas yang meningkat melahirkan proliferasi istilah: metrocell, metro femtocell, femtocell akses publik, femtocell perusahaan, super femtos, femto kelas 3, femtos lebih besar dan microcell. Istilah “sel-sel kecil” sering digunakan oleh analis dan industri sebagai payung untuk menggambarkan implementasi yang berbeda dari femtocell, dan untuk menjernihkan kebingungan bahwa femtocell terbatas untuk penggunaan di rumah. Sel kecil kadang-kadang, secara keliru, juga digunakan untuk menggambarkan sistem antena terdistribusi (DAS) yang bukan node akses bertenaga rendah.

Tujuan

Sel kecil dapat digunakan untuk menyediakan layanan nirkabel di dalam dan di luar ruangan. Operator seluler menggunakannya untuk memperluas jangkauan layanan mereka dan / atau meningkatkan kapasitas jaringan .

ABI Research berpendapat bahwa sel-sel kecil juga membantu penyedia layanan menemukan peluang pendapatan baru melalui informasi lokasi dan keberadaan mereka . Jika pengguna terdaftar memasuki femtozone, jaringan diberitahu tentang lokasi mereka. Penyedia layanan, dengan izin pengguna, dapat membagikan informasi lokasi ini untuk memperbarui status media sosial pengguna, misalnya. Membuka API sel kecil ke ekosistem seluler yang lebih luas dapat mengaktifkan efek jangka panjang .

Cakupan pedesaan juga merupakan pasar utama yang telah berkembang karena operator seluler telah mulai memasang metrosel akses publik di daerah terpencil dan pedesaan yang hanya memiliki cakupan 2G atau tidak memiliki jangkauan sama sekali. Keuntungan biaya sel kecil dibandingkan dengan sel makro membuatnya layak secara ekonomi untuk menyediakan cakupan komunitas yang jauh lebih kecil – dari beberapa sepuluh hingga beberapa ratus. Small Cell Forum telah menerbitkan buku putih yang menguraikan aspek teknologi dan kasus bisnis. Operator seluler di negara berkembang dan maju mencoba atau menginstal sistem seperti itu. Pelopor dalam menyediakan cakupan pedesaan menggunakan sel kecil adalah SoftBank Mobile – operator seluler Jepang – yang telah menginstal lebih dari 3000 sel publik akses 3G kecil di kantor pos di seluruh pedesaan Jepang. Di Inggris, program Sinyal Terbuka Pedesaan Vodafone dan skema pedesaan 3G / 4G EE meningkatkan cakupan geografis.

Jaringan Seluler Masa Depan

Sel kecil adalah bagian integral dari jaringan LTE di masa depan. Dalam jaringan 3G, sel-sel kecil dipandang sebagai teknik pembongkaran . Dalam jaringan 4G, prinsip jaringan heterogen (HetNet) diperkenalkan di mana jaringan seluler dibangun dengan lapisan sel kecil dan besar. Dalam LTE, semua sel akan mengatur dirinya sendiri, berdasarkan prinsip-prinsip yang ditetapkan dalam Home NodeB (HNB) saat ini, istilah 3GPP untuk femtocell residensial.

Inovasi masa depan dalam desain akses radio memperkenalkan gagasan tentang arsitektur yang hampir datar di mana perbedaan antara sel kecil dan sel makro tergantung pada berapa banyak kubus yang ditumpuk menjadi satu. Sinyal transmisi dari MBS melemah dengan cepat begitu sinyal Stasiun Basis Makro (MBS) mencapai dalam ruangan. Femtocell memberikan solusi untuk kesulitan yang ada dalam sistem berbasis macrocell. Dengan demikian, jangkauan jaringan Femto Base Station (FBS) adalah salah satu perhatian utama dalam lingkungan dalam ruangan untuk mendapatkan kualitas layanan yang baik (QoS).

Backhaul Sel Kecil

Backhaul diperlukan untuk menghubungkan sel-sel kecil ke jaringan inti, internet dan layanan lainnya. Untuk penggunaan dalam gedung, internet broadband yang ada dapat digunakan. Di perkotaan terbuka, operator seluler menganggap ini lebih menantang daripada backhaul macrocell karena a) sel kecil biasanya berada di lokasi yang sulit dijangkau, di dekat jalan daripada di lokasi yang lebih terbuka, di atas atap dan b) konektivitas tingkat operator harus disediakan dengan biaya yang jauh lebih rendah per bit. Banyak teknologi nirkabel dan kabel yang berbeda telah diusulkan sebagai solusi, dan disepakati bahwa ‘kotak peralatan’ ini diperlukan untuk mengatasi berbagai skenario penggunaan. Pandangan konsensus industri tentang bagaimana karakteristik solusi yang berbeda sesuai dengan persyaratan diterbitkan oleh Small Cell Forum. Solusi backhaul dipengaruhi oleh sejumlah faktor, termasuk motivasi asli operator untuk mengerahkan sel-sel kecil, yang bisa untuk kapasitas yang ditargetkan, cakupan dalam atau luar ruangan.

Daftar Pustaka

https://en.wikipedia.org/wiki/Gigabit_Wireless
https://en.wikipedia.org/wiki/Small_cell

Radiasi Elektromagnetik

light_dispersion_conceptual_waves

Radiasi elektromagnetik sinar putih dalam sebuah prisma (optik) yang terurai menjadi beberapa warna cahaya yang terpisah

Radiasi elektromagnetik adalah kombinasi medan listrik dan medan magnet yang berosilasi dan merambat melewati ruang dan membawa energi dari satu tempat ke tempat yang lain. Cahaya tampak adalah salah satu bentuk radiasi elektromagnetik. Penelitian teoretis tentang radiasi elektromagnetik disebut elektrodinamik, sub-bidang elektromagnetisme. Gelombang elektromagnetik ditemukan oleh Heinrich Hertz. Gelombang elektromagnetik termasuk gelombang transversal.

Setiap muatan listrik yang memiliki percepatan memancarkan radiasi elektromagnetik. Ketika kawat (atau panghantar seperti antena) menghantarkan arus bolak-balik, radiasi elektromagnetik dirambatkan pada frekuensi yang sama dengan arus listrik. Bergantung pada situasi, gelombang elektromagnetik dapat bersifat seperti gelombang atau seperti partikel. Sebagai gelombang, dicirikan oleh kecepatan (kecepatan cahaya), panjang gelombang, dan frekuensi. Kalau dipertimbangkan sebagai partikel, mereka diketahui sebagai foton, dan masing-masing mempunyai energi berhubungan dengan frekuensi gelombang ditunjukan oleh hubungan Planck E = Hf, di mana E adalah energi foton, h ialah konstanta Planck — 6.626 × 10 −34 J·s — dan f adalah frekuensi gelombang. Einstein kemudian memperbarui rumus ini menjadi Ephoton = hf.

Yang termasuk gelombang elektromagnetik

Gelombang	Panjang gelombang λ
gelombang radio	1 mm-10.000 km
infra merah	0,001–1 mm
spektrum kasatmata	400-720 nm
ultra violet	10-400 nm
sinar X	0,01-10 nm
sinar gamma	0,0001-0,1 nm

electromagnetic-spectrum

Spektrum elektromagnetik

Sinar kosmis tidak termasuk gelombang elektromagnetik; panjang gelombang lebih kecil dari 0,0001 nm.

Sinar dengan panjang gelombang besar, yaitu gelombang radio dan infra merah, mempunyai frekuensi dan tingkat energi yang lebih rendah. Sinar dengan panjang gelombang kecil, ultra violet, sinar x atau sinar rontgen, dan sinar gamma, mempunyai frekuensi dan tingkat energi yang lebih tinggi.

Transformasi Wavelet

Teori wavelet adalah suatu konsep yang relatif baru dikembangkan. Kata “Wavelet” sendiri diberikan oleh Jean Morlet dan Alex Grossmann pada awal tahun 1980-an, dan berasal dari bahasa Prancis, “ondelette” yang berarti gelombang kecil. Kata “onde” yang berarti gelombang kemudian diterjemahkan ke bahasa Inggris menjadi “wave”, lalu digabung dengan kata aslinya sehingga terbentuk kata baru “wavelet”. Transformasi wavelet dibagi menjadi dua bagian besar, yaitu transformasi wavelet kontinu (TWK) dan transformasi wavelet diskrit (TWD).

Perbandingan dengan Transformasi Fourier

Sampai sekarang transformasi Fourier mungkin masih menjadi transformasi yang paling populer di area pemrosesan sinyal digital (PSD). Transformasi Fourier memberitahu kita informasi frekuensi dari sebuah sinyal, tapi tidak informasi waktu (kita tidak dapat tahu di mana frekuensi itu terjadi).

Karena itulah transformasi Fourier hanya cocok untuk sinyal stationari (sinyal yang informasi frekuensinya tidak berubah menurut waktu). Untuk menganalisa sinyal yang frekuensinya bervariasi di dalam waktu, diperlukan suatu transformasi yang dapat memberikan resolusi frekuensi dan waktu disaat yang bersamaan, biasa disebut analisis multi resolusi (AMR). AMR dirancang untuk memberika resolusi waktu yang baik dan resolusi frekuensi yang buruk pada frekuensi tinggi suatu sinyal, serta resolusi frekuensi yang baik dan resolusi waktu yang buruk pada frekuensi rendah suatu sinyal. Pendekatan ini sangat berguna untuk menganalisa sinyal dalam aplikasi-aplikasi praktis yang memang memiliki lebih banyak frekuensi rendah.

Transformasi wavelet adalah suatu AMR yang dapat merepresentasikan informasi waktu dan frekuensi suatu sinyal dengan baik. Transformasi wavelet menggunakan sebuah jendela modulasi yang fleksibel, ini yang paling membedakannya dengan transformasi Fourier waktu-singkat (STFT), yang merupakan pengembangan dari transformasi Fourier. STFT menggunakan jendela modulasi yang besarnya tetap, ini menyebabkan dilema karena jendela yang sempit akan memberikan resolusi frekuensi yang buruk dan sebaliknya jendela yang lebar akan menyebabkan resolusi waktu yang buruk.

Transformasi Wavelet Kontinu

Cara kerja transformasi wavelet kontinu (TWK) adalah dengan menghitung konvolusi sebuah sinyal dengan sebuah jendela modulasi pada setiap waktu dengan setiap skala yang diinginkan. Jendela modulasi yang mempunyai skala fleksibel inilah yang biasa disebut induk wavelet atau fungsi dasar wavelet.

Dalam transformasi wavelet digunakan istilah translasi dan skala, karena istilah waktu dan frekuensi sudah digunakan oleh transformasi Fourier. Translasi adalah lokasi jendela modulasi saat digeser sepanjang sinyal, berhubungan dengan informasi waktu. Skala behubungan dengan frekuensi, skala tinggi (frekuensi rendah) berhubungan dengan informasi global dari sebuah sinyal, sedangkan skala rendah (frekuensi tinggi) berhubungan dengan informasi detail.

TWK secara matematika dapat didefinisikan sebagai berikut:

\gamma (s,\tau )=\int f(t)\psi _{s,\tau }^{*}(t)dt

Keterangan: $\gamma (s,\tau )$ adalah fungsi sinyal setelah transformasi, dengan variabel s (skala) dan $\tau$ (translasi) sebagai dimensi baru. $f(t)$ sinyal asli sebelum transformasi. Fungsi dasar $\psi _{s,\tau }^{*}(t)$ di sebut sebagai wavelet, dengan * menunjukkan konjugasi kompleks.

Dan inversi dari TWK secara matematika dapat didefinisikan sebagai berikut:

f(t)=\int \int \gamma (s,\tau )\psi _{s,\tau }(t)d\tau ds

Seperti telah dibicarakan sebelumnya, fungsi dasar wavelet $\psi _{s,\tau }(t)$ dapat didesain sesuai kebutuhan untuk mendapatkan hasil transformasi yang terbaik, ini perbedaan mendasar dengan transformasi Fourier yang hanya menggunakan fungsi sinus sebagai jendela modulasi.

Fungsi dasar wavelet secara matematika dapat didefinisikan sebagi berikut:

\psi _{s,\tau }(t)={\frac {1}{\sqrt {s}}}\psi \left({\frac {t-\tau }{s}}\right)

${\frac {1}{\sqrt {s}}}$ digunakan untuk normalisasi energi pada skala yang berubah-ubah.

Mexican Hat, yang merupakan normalisasi dari derivatif kedua fungsi Gaussian adalah salah satu contoh fungsi dasar TWK:

\psi (t)={1 \over {{\sqrt {2\pi }}\sigma ^{3}}}\left(1-{t^{2} \over \sigma ^{2}}\right)e^{-t^{2} \over 2\sigma ^{2}}

Contoh lain adalah fungsi dasar Morlet, yang merupakan fungsi bilangan kompleks:

\psi _{\sigma }(t)=c_{\sigma }\pi ^{-{\frac {1}{4}}}e^{-{\frac {1}{2}}t^{2}}(e^{i\sigma t}-\kappa _{\sigma })

dengan $\kappa _{\sigma }=e^{-{\frac {1}{2}}\sigma ^{2}}$ dan $c_{\sigma }=\left(1+e^{-\sigma ^{2}}-2e^{-{\frac {3}{4}}\sigma ^{2}}\right)^{-{\frac {1}{2}}}$

Wavelet Mexican Hat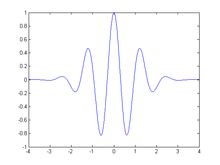

Wavelet Morlet

Transformasi Wavelet Diskrit

Dibandingkan dengan TWK, transformasi wavelet diskrit (TWD) dianggap relatif lebih mudah pengimplementasiannya. Prinsip dasar dari TWD adalah bagaimana cara mendapatkan representasi waktu dan skala dari sebuah sinyal menggunakan teknik pemfilteran digital dan operasi sub-sampling.

Sinyal pertama-tama dilewatkan pada rangkain filter high-pass dan low-pass, kemudian setengah dari masing-masing keluaran diambil sebagai sample melalui operasi sub-sampling. Proses ini disebut sebagai proses dekomposisi satu tingkat. Keluaran dari filter low-pass digunakan sebagai masukkan di proses dekomposisi tingkat berikutnya. Proses ini diulang sampai tingkat proses dekomposisi yang diinginkan. Gabungan dari keluaran-keluaran filter high-pass dan satu keluaran filter low-pass yang terakhir, disebut sebagai koefisien wavelet, yang berisi informasi sinyal hasil transformasi yang telah terkompresi.

Berkat operasi sub-sampling yang menghilangkan informasi sinyal yang berlebihan, transformasi wavelet telah menjadi salah satu metode kompresi data yang paling handal. Biro investigasi federal (FBI) Amerika Serikat menggunakan metode ini dalam proses kompresi data sidik jari mereka.

Pasangan filter high-pass dan low-pass yang digunakan harus merupakan quadrature mirror filter (QMF), yaitu pasangan filter yang memenuhi persamaan berikut:

h [ L − 1 − n ] = ( − 1 ) n ⋅ g [ n ]

dengan h[n] adalah filtar high-pass, g[n] adalah filter low-pass dan L adalah panjang masing-masing filter

Short Time Fourier Transform

Contoh waktu singkat Transformasi Fourier digunakan untuk menentukan waktu dampak dari sinyal audio

Transformasi Fourier waktu-pendek (STFT), adalah transformasi terkait-Fourier yang digunakan untuk menentukan frekuensi sinusoidal dan konten fase dari bagian-bagian lokal dari suatu sinyal saat ia berubah dari waktu ke waktu. Dalam praktiknya, prosedur untuk menghitung STFT adalah membagi sinyal waktu yang lebih panjang menjadi segmen yang lebih pendek dengan panjang yang sama dan kemudian menghitung transformasi Fourier secara terpisah pada setiap segmen yang lebih pendek. Ini mengungkapkan spektrum Fourier pada setiap segmen yang lebih pendek. Satu kemudian biasanya plot perubahan spektrum sebagai fungsi waktu.

STFT waktu kontinu
Sederhananya, dalam kasus waktu kontinu, fungsi yang akan diubah dikalikan dengan fungsi jendela yang bukan nol hanya untuk periode waktu yang singkat. Transformasi Fourier (fungsi satu dimensi) dari sinyal yang dihasilkan diambil ketika jendela digeser sepanjang sumbu waktu, menghasilkan representasi sinyal dua dimensi. Secara matematis, ini ditulis sebagai:

$\mathbf {STFT} \{x(t)\}(\tau ,\omega )\equiv X(\tau ,\omega )=\int _{-\infty }^{\infty }x(t)w(t-\tau )e^{-j\omega t}\,dt$

di mana w (t) adalah fungsi jendela, umumnya jendela Hann atau jendela Gaussian berpusat di sekitar nol, dan x (t) adalah sinyal yang akan diubah [rujukan?] (perhatikan perbedaan antara w dan ω). X (τ, ω) pada dasarnya adalah Fourier Transform dari x (t) w (t-τ), fungsi kompleks yang mewakili fase dan besarnya sinyal dari waktu ke waktu dan frekuensi. Seringkali pembungkusan fase digunakan di sepanjang salah satu atau kedua sumbu waktu, τ, dan sumbu frekuensi, ω, untuk menekan setiap ketidaksinambungan lompatan dari hasil fase STFT. Indeks waktu τ biasanya dianggap sebagai waktu “lambat” dan biasanya tidak dinyatakan dalam resolusi setinggi waktu t.

STFT waktu diskrit
Dalam kasus waktu diskrit, data yang akan ditransformasikan dapat dipecah menjadi potongan-potongan atau bingkai (yang biasanya saling tumpang tindih, untuk mengurangi artefak di batas). Setiap bongkahan adalah transformasi Fourier, dan hasil kompleks ditambahkan ke matriks, yang merekam besarnya dan fase untuk setiap titik dalam waktu dan frekuensi. Ini dapat dinyatakan sebagai:

$\mathbf {STFT} \{x[n]\}(m,\omega )\equiv X(m,\omega )=\sum _{n=-\infty }^{\infty }x[n]w[n-m]e^{-j\omega n}$

demikian juga dengan sinyal x [n] dan jendela w [n]. Dalam hal ini, m adalah diskrit dan ω kontinu, tetapi dalam sebagian besar aplikasi STFT dilakukan pada komputer menggunakan Fast Fourier Transform, sehingga kedua variabel diskrit dan terkuantisasi.
Besarnya kuadrat dari STFT menghasilkan representasi spektrogram dari Power Spectral Density dari fungsi:

$\operatorname {spectrogram} \{x(t)\}(\tau ,\omega )\equiv |X(\tau ,\omega )|^{2}$

Lihat juga transformasi cosine diskrit yang dimodifikasi (MDCT), yang juga merupakan transformasi terkait Fourier yang menggunakan jendela yang tumpang tindih.

Geser DFT
Jika hanya sejumlah kecil ω yang diinginkan, atau jika STFT ingin dievaluasi untuk setiap m pergeseran jendela, maka STFT mungkin lebih efisien dievaluasi menggunakan algoritma DFT geser.

STFT terbalik
STFT tidak dapat dibalik, yaitu, sinyal asli dapat dipulihkan dari transformasi oleh STFT Invers. Cara yang paling banyak diterima untuk membalikkan STFT adalah dengan menggunakan metode overlap-add (OLA), yang juga memungkinkan untuk modifikasi pada spektrum kompleks STFT. Ini membuat metode pemrosesan sinyal serbaguna, disebut sebagai tumpang tindih dan ditambahkan dengan metode modifikasi.
Mengingat lebar dan definisi fungsi jendela w (t), pada awalnya kami membutuhkan area fungsi jendela untuk diskalakan sehingga

STFT waktu kontinu

Mengingat lebar dan definisi fungsi jendela w (t), pada awalnya kami membutuhkan area fungsi jendela untuk diskalakan sehingga

$\int _{-\infty }^{\infty }w(\tau )\,d\tau =1.$

Dengan mudah mengikuti itu

$\int _{-\infty }^{\infty }w(t-\tau )\,d\tau =1\quad \forall \ t$

dan

$x(t)=x(t)\int _{-\infty }^{\infty }w(t-\tau )\,d\tau =\int _{-\infty }^{\infty }x(t)w(t-\tau )\,d\tau .$

Transformasi Fourier kontinu adalah

$X(\omega )=\int _{-\infty }^{\infty }x(t)e^{-j\omega t}\,dt.$

Mengganti x (t) dari atas:

$X(\omega )=\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }x(t)w(t-\tau )\,d\tau \right]\,e^{-j\omega t}\,dt$

$=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }x(t)w(t-\tau )\,e^{-j\omega t}\,d\tau \,dt.$

Urutan pertukaran integrasi:

$X(\omega )=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }x(t)w(t-\tau )\,e^{-j\omega t}\,dt\,d\tau$

$=\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }x(t)w(t-\tau )\,e^{-j\omega t}\,dt\right]\,d\tau$

$=\int _{-\infty }^{\infty }X(\tau ,\omega )\,d\tau .$

Jadi Transformasi Fourier dapat dilihat sebagai semacam jumlah fase yang koheren dari semua STFTs x (t). Karena transformasi Fourier terbalik adalah

$x(t)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }X(\omega )e^{+j\omega t}\,d\omega ,$

then x(t) can be recovered from X(τ,ω) as

$x(t)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }X(\tau ,\omega )e^{+j\omega t}\,d\tau \,d\omega .$

atau

$x(t)=\int _{-\infty }^{\infty }\left[{\frac {1}{2\pi }}\int _{-\infty }^{\infty }X(\tau ,\omega )e^{+j\omega t}\,d\omega \right]\,d\tau .$

Dapat dilihat, dibandingkan dengan di atas bahwa “butir” berjendela atau “wavelet” dari x (t) adalah

$x(t)w(t-\tau )={\frac {1}{2\pi }}\int _{-\infty }^{\infty }X(\tau ,\omega )e^{+j\omega t}\,d\omega .$

transformasi Fourier terbalik X (τ, ω) untuk τ tetap.

Masalah resolusi

Salah satu perangkap STFT adalah bahwa ia memiliki resolusi tetap. Lebar fungsi windowing berkaitan dengan bagaimana sinyal diwakili — itu menentukan apakah ada resolusi frekuensi yang baik (komponen frekuensi yang berdekatan dapat dipisahkan) atau resolusi waktu yang baik (waktu di mana frekuensi berubah). Jendela lebar memberikan resolusi frekuensi yang lebih baik tetapi resolusi waktu yang buruk. Jendela yang lebih sempit memberikan resolusi waktu yang baik tetapi resolusi frekuensi yang buruk. Ini disebut narrowband dan wideband transforms, masing-masing.

Perbandingan resolusi STFT. Kiri memiliki resolusi waktu yang lebih baik, dan kanan memiliki resolusi frekuensi yang lebih baik.

Ini adalah salah satu alasan untuk menciptakan transformasi wavelet dan analisis multiresolusi, yang dapat memberikan resolusi waktu yang baik untuk peristiwa frekuensi tinggi dan resolusi frekuensi yang baik untuk peristiwa frekuensi rendah, kombinasi yang paling cocok untuk banyak sinyal nyata.
Properti ini terkait dengan prinsip ketidakpastian Heisenberg, tetapi tidak secara langsung – lihat batas Gabor untuk diskusi. Produk standar deviasi dalam waktu dan frekuensi terbatas. Batas prinsip ketidakpastian (resolusi simultan terbaik dari keduanya) dicapai dengan fungsi jendela Gaussian, karena Gaussian meminimalkan prinsip ketidakpastian Fourier. Ini disebut transformasi Gabor (dan dengan modifikasi untuk multiresolusi menjadi transformasi wavelet Morlet).
Seseorang dapat mempertimbangkan STFT untuk memvariasikan ukuran jendela sebagai domain dua dimensi (waktu dan frekuensi), seperti yang diilustrasikan dalam contoh di bawah ini, yang dapat dihitung dengan memvariasikan ukuran jendela. Namun, ini bukan lagi representasi frekuensi waktu – kernel tidak konstan di seluruh sinyal.

Contoh : Dengan menggunakan sinyal sampel x berikut (t) {\ displaystyle x (t)} x (t) yang terdiri dari seperangkat empat bentuk gelombang sinusoidal yang bergabung bersama secara berurutan. Setiap gelombang hanya terdiri dari satu dari empat frekuensi (10, 25, 50, 100 Hz). Definisi x (t) {\ displaystyle x (t)} x (t) adalah:

$x(t)={\begin{cases}\cos(2\pi 10t)&0\,\mathrm {s} \leq t<5\,\mathrm {s} \\\cos(2\pi 25t)&5\,\mathrm {s} \leq t<10\,\mathrm {s} \\\cos(2\pi 50t)&10\,\mathrm {s} \leq t<15\,\mathrm {s} \\\cos(2\pi 100t)&15\,\mathrm {s} \leq t<20\,\mathrm {s} \\\end{cases}}$

Kemudian diambil sampelnya pada 400 Hz. Spektrogram berikut diproduksi:

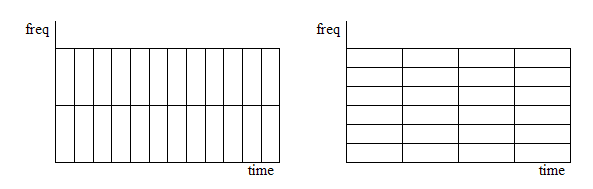
25 ms window

125 ms window

375 ms window

1000 ms window

Jendela 25 ms memungkinkan kita untuk mengidentifikasi waktu yang tepat di mana sinyal berubah tetapi frekuensi yang tepat sulit untuk diidentifikasi. Di ujung lain skala, jendela 1000 ms memungkinkan frekuensi untuk dilihat secara tepat tetapi waktu antara perubahan frekuensi kabur.

sumber : https://en.wikipedia.org/wiki/Short-time_Fourier_transform

Tri Khaerudin

Halaman