Tri Khaerudin: Short Time Fourier Transform

Contoh waktu singkat Transformasi Fourier digunakan untuk menentukan waktu dampak dari sinyal audio

Transformasi Fourier waktu-pendek (STFT), adalah transformasi terkait-Fourier yang digunakan untuk menentukan frekuensi sinusoidal dan konten fase dari bagian-bagian lokal dari suatu sinyal saat ia berubah dari waktu ke waktu. Dalam praktiknya, prosedur untuk menghitung STFT adalah membagi sinyal waktu yang lebih panjang menjadi segmen yang lebih pendek dengan panjang yang sama dan kemudian menghitung transformasi Fourier secara terpisah pada setiap segmen yang lebih pendek. Ini mengungkapkan spektrum Fourier pada setiap segmen yang lebih pendek. Satu kemudian biasanya plot perubahan spektrum sebagai fungsi waktu.

STFT waktu kontinu
Sederhananya, dalam kasus waktu kontinu, fungsi yang akan diubah dikalikan dengan fungsi jendela yang bukan nol hanya untuk periode waktu yang singkat. Transformasi Fourier (fungsi satu dimensi) dari sinyal yang dihasilkan diambil ketika jendela digeser sepanjang sumbu waktu, menghasilkan representasi sinyal dua dimensi. Secara matematis, ini ditulis sebagai:

$\mathbf {STFT} \{x(t)\}(\tau ,\omega )\equiv X(\tau ,\omega )=\int _{-\infty }^{\infty }x(t)w(t-\tau )e^{-j\omega t}\,dt$

di mana w (t) adalah fungsi jendela, umumnya jendela Hann atau jendela Gaussian berpusat di sekitar nol, dan x (t) adalah sinyal yang akan diubah [rujukan?] (perhatikan perbedaan antara w dan ω). X (τ, ω) pada dasarnya adalah Fourier Transform dari x (t) w (t-τ), fungsi kompleks yang mewakili fase dan besarnya sinyal dari waktu ke waktu dan frekuensi. Seringkali pembungkusan fase digunakan di sepanjang salah satu atau kedua sumbu waktu, τ, dan sumbu frekuensi, ω, untuk menekan setiap ketidaksinambungan lompatan dari hasil fase STFT. Indeks waktu τ biasanya dianggap sebagai waktu “lambat” dan biasanya tidak dinyatakan dalam resolusi setinggi waktu t.

STFT waktu diskrit
Dalam kasus waktu diskrit, data yang akan ditransformasikan dapat dipecah menjadi potongan-potongan atau bingkai (yang biasanya saling tumpang tindih, untuk mengurangi artefak di batas). Setiap bongkahan adalah transformasi Fourier, dan hasil kompleks ditambahkan ke matriks, yang merekam besarnya dan fase untuk setiap titik dalam waktu dan frekuensi. Ini dapat dinyatakan sebagai:

$\mathbf {STFT} \{x[n]\}(m,\omega )\equiv X(m,\omega )=\sum _{n=-\infty }^{\infty }x[n]w[n-m]e^{-j\omega n}$

demikian juga dengan sinyal x [n] dan jendela w [n]. Dalam hal ini, m adalah diskrit dan ω kontinu, tetapi dalam sebagian besar aplikasi STFT dilakukan pada komputer menggunakan Fast Fourier Transform, sehingga kedua variabel diskrit dan terkuantisasi.
Besarnya kuadrat dari STFT menghasilkan representasi spektrogram dari Power Spectral Density dari fungsi:

$\operatorname {spectrogram} \{x(t)\}(\tau ,\omega )\equiv |X(\tau ,\omega )|^{2}$

Lihat juga transformasi cosine diskrit yang dimodifikasi (MDCT), yang juga merupakan transformasi terkait Fourier yang menggunakan jendela yang tumpang tindih.

Geser DFT
Jika hanya sejumlah kecil ω yang diinginkan, atau jika STFT ingin dievaluasi untuk setiap m pergeseran jendela, maka STFT mungkin lebih efisien dievaluasi menggunakan algoritma DFT geser.

STFT terbalik
STFT tidak dapat dibalik, yaitu, sinyal asli dapat dipulihkan dari transformasi oleh STFT Invers. Cara yang paling banyak diterima untuk membalikkan STFT adalah dengan menggunakan metode overlap-add (OLA), yang juga memungkinkan untuk modifikasi pada spektrum kompleks STFT. Ini membuat metode pemrosesan sinyal serbaguna, disebut sebagai tumpang tindih dan ditambahkan dengan metode modifikasi.
Mengingat lebar dan definisi fungsi jendela w (t), pada awalnya kami membutuhkan area fungsi jendela untuk diskalakan sehingga

STFT waktu kontinu

Mengingat lebar dan definisi fungsi jendela w (t), pada awalnya kami membutuhkan area fungsi jendela untuk diskalakan sehingga

$\int _{-\infty }^{\infty }w(\tau )\,d\tau =1.$

Dengan mudah mengikuti itu

$\int _{-\infty }^{\infty }w(t-\tau )\,d\tau =1\quad \forall \ t$

dan

$x(t)=x(t)\int _{-\infty }^{\infty }w(t-\tau )\,d\tau =\int _{-\infty }^{\infty }x(t)w(t-\tau )\,d\tau .$

Transformasi Fourier kontinu adalah

$X(\omega )=\int _{-\infty }^{\infty }x(t)e^{-j\omega t}\,dt.$

Mengganti x (t) dari atas:

$X(\omega )=\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }x(t)w(t-\tau )\,d\tau \right]\,e^{-j\omega t}\,dt$

$=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }x(t)w(t-\tau )\,e^{-j\omega t}\,d\tau \,dt.$

Urutan pertukaran integrasi:

$X(\omega )=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }x(t)w(t-\tau )\,e^{-j\omega t}\,dt\,d\tau$

$=\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }x(t)w(t-\tau )\,e^{-j\omega t}\,dt\right]\,d\tau$

$=\int _{-\infty }^{\infty }X(\tau ,\omega )\,d\tau .$

Jadi Transformasi Fourier dapat dilihat sebagai semacam jumlah fase yang koheren dari semua STFTs x (t). Karena transformasi Fourier terbalik adalah

$x(t)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }X(\omega )e^{+j\omega t}\,d\omega ,$

then x(t) can be recovered from X(τ,ω) as

$x(t)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }X(\tau ,\omega )e^{+j\omega t}\,d\tau \,d\omega .$

atau

$x(t)=\int _{-\infty }^{\infty }\left[{\frac {1}{2\pi }}\int _{-\infty }^{\infty }X(\tau ,\omega )e^{+j\omega t}\,d\omega \right]\,d\tau .$

Dapat dilihat, dibandingkan dengan di atas bahwa “butir” berjendela atau “wavelet” dari x (t) adalah

$x(t)w(t-\tau )={\frac {1}{2\pi }}\int _{-\infty }^{\infty }X(\tau ,\omega )e^{+j\omega t}\,d\omega .$

transformasi Fourier terbalik X (τ, ω) untuk τ tetap.

Masalah resolusi

Salah satu perangkap STFT adalah bahwa ia memiliki resolusi tetap. Lebar fungsi windowing berkaitan dengan bagaimana sinyal diwakili — itu menentukan apakah ada resolusi frekuensi yang baik (komponen frekuensi yang berdekatan dapat dipisahkan) atau resolusi waktu yang baik (waktu di mana frekuensi berubah). Jendela lebar memberikan resolusi frekuensi yang lebih baik tetapi resolusi waktu yang buruk. Jendela yang lebih sempit memberikan resolusi waktu yang baik tetapi resolusi frekuensi yang buruk. Ini disebut narrowband dan wideband transforms, masing-masing.

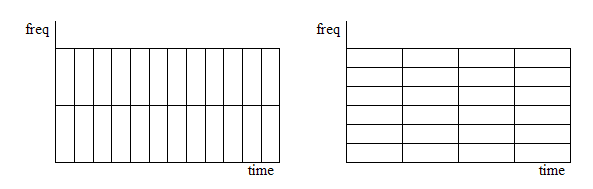
Perbandingan resolusi STFT. Kiri memiliki resolusi waktu yang lebih baik, dan kanan memiliki resolusi frekuensi yang lebih baik.

Ini adalah salah satu alasan untuk menciptakan transformasi wavelet dan analisis multiresolusi, yang dapat memberikan resolusi waktu yang baik untuk peristiwa frekuensi tinggi dan resolusi frekuensi yang baik untuk peristiwa frekuensi rendah, kombinasi yang paling cocok untuk banyak sinyal nyata.
Properti ini terkait dengan prinsip ketidakpastian Heisenberg, tetapi tidak secara langsung – lihat batas Gabor untuk diskusi. Produk standar deviasi dalam waktu dan frekuensi terbatas. Batas prinsip ketidakpastian (resolusi simultan terbaik dari keduanya) dicapai dengan fungsi jendela Gaussian, karena Gaussian meminimalkan prinsip ketidakpastian Fourier. Ini disebut transformasi Gabor (dan dengan modifikasi untuk multiresolusi menjadi transformasi wavelet Morlet).
Seseorang dapat mempertimbangkan STFT untuk memvariasikan ukuran jendela sebagai domain dua dimensi (waktu dan frekuensi), seperti yang diilustrasikan dalam contoh di bawah ini, yang dapat dihitung dengan memvariasikan ukuran jendela. Namun, ini bukan lagi representasi frekuensi waktu – kernel tidak konstan di seluruh sinyal.

Contoh : Dengan menggunakan sinyal sampel x berikut (t) {\ displaystyle x (t)} x (t) yang terdiri dari seperangkat empat bentuk gelombang sinusoidal yang bergabung bersama secara berurutan. Setiap gelombang hanya terdiri dari satu dari empat frekuensi (10, 25, 50, 100 Hz). Definisi x (t) {\ displaystyle x (t)} x (t) adalah:

$x(t)={\begin{cases}\cos(2\pi 10t)&0\,\mathrm {s} \leq t<5\,\mathrm {s} \\\cos(2\pi 25t)&5\,\mathrm {s} \leq t<10\,\mathrm {s} \\\cos(2\pi 50t)&10\,\mathrm {s} \leq t<15\,\mathrm {s} \\\cos(2\pi 100t)&15\,\mathrm {s} \leq t<20\,\mathrm {s} \\\end{cases}}$

Kemudian diambil sampelnya pada 400 Hz. Spektrogram berikut diproduksi:

25 ms window

125 ms window

375 ms window

1000 ms window

Jendela 25 ms memungkinkan kita untuk mengidentifikasi waktu yang tepat di mana sinyal berubah tetapi frekuensi yang tepat sulit untuk diidentifikasi. Di ujung lain skala, jendela 1000 ms memungkinkan frekuensi untuk dilihat secara tepat tetapi waktu antara perubahan frekuensi kabur.

sumber : https://en.wikipedia.org/wiki/Short-time_Fourier_transform

Tri Khaerudin

Halaman

Jumat, 29 Mei 2020

Short Time Fourier Transform

Tidak ada komentar:

Posting Komentar

Blog Archive

Entri yang Diunggulkan

Tahukah anda perusahaan selain Cisco, ternyata ada Aruba Networks!!!

Arsip Blog